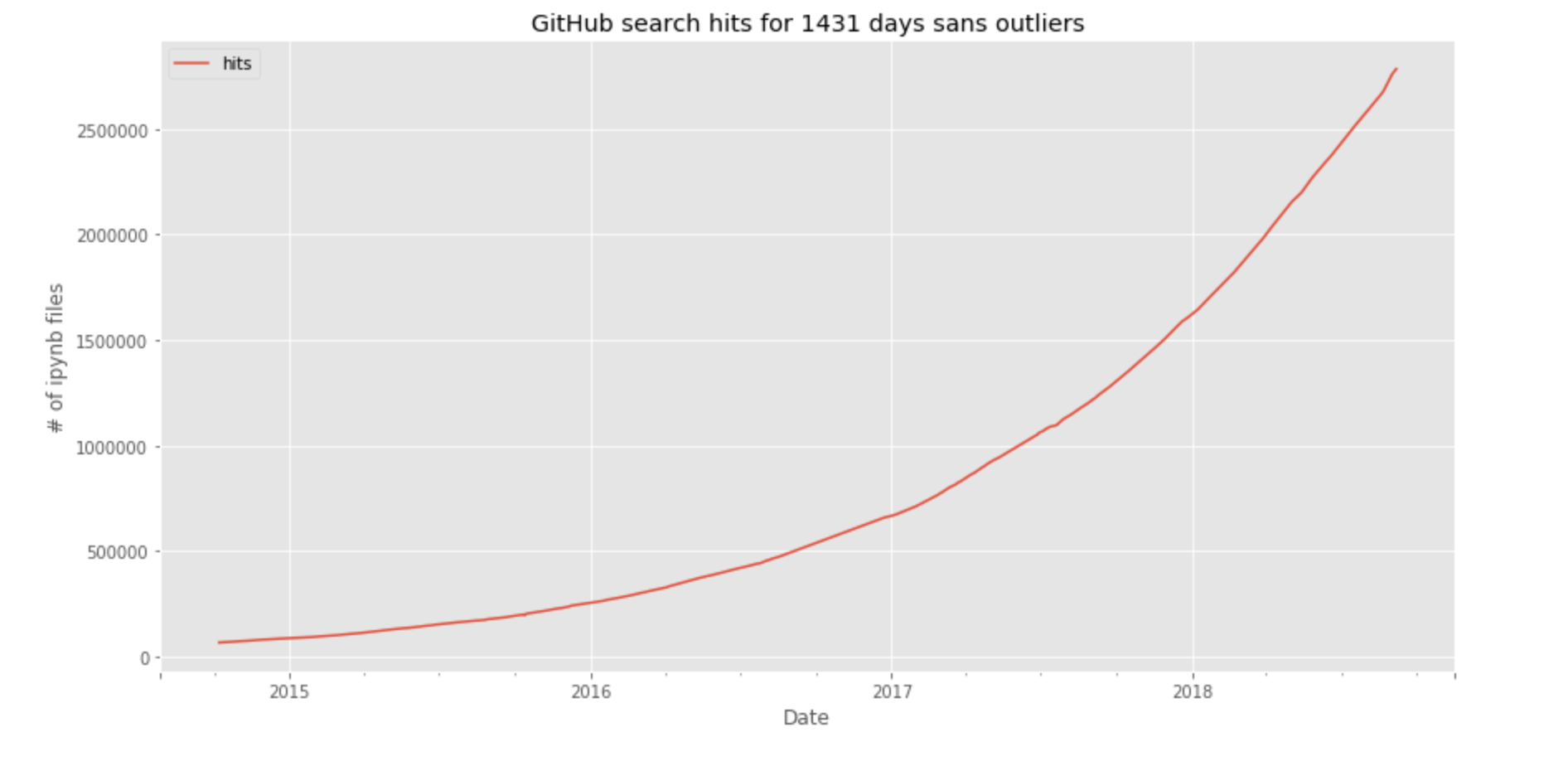
STA2453 - Data Science Methods, Collaboration, and Communication¶
Class #1¶
September 10, 2019¶
Professor Nathan Taback
office: SS6027C
e-mail: nathan.taback@utoronto.ca
office hours: TBD
Course website: https://sta2453.github.io
Course Overview¶
The primary learning objectives are:
- to gain experience using data analysis to extract information.
- to gain experience communicating information that arise from a data analysis.
But, not everyone ...
What is data analysis?¶
These quotes are from Tukey's 1962 paper, The Future of Data Analysis.
... data analysis, which I take to include, among other things: procedures for analyzing data, techniques for interpreting the results of such procedures, ways of planning the gathering of data to make its analysis easier, more precise or more accurate, and all the machinery and results of (mathematical) statistics which apply to analyzing data.
Data analysis ... take on the chracteristics of a science rather than those of mathematics ...

Roger Peng states that
If one were to write down the steps in a data analysis, you might come up with something along these lines of the following list
- Defining the question
- Defining the ideal dataset
- Determining what data you can access
- Obtaining the data
- Cleaning the data
- Exploratory data analysis
- Statistical prediction/modeling
- Interpretation of results
- Challenging of results
- Synthesis and write up
- Creating reproducible code
Computing¶
I use R and Python. RStudio and Jupyter notebooks are excellent tools.
I expect that all work will be done in a "reproducible" manner.
library(tidyverse)
library(repr)
options(repr.plot.width=4, repr.plot.height=3)
suppressPackageStartupMessages(library(tidyverse))
agedat <- tibble(age = c(25, 20, 21, 120, 19, 31, 90, 17), sex = c(rep("Male", 4), rep("Female", 4)))
ggplot(agedat, aes(sex, age)) + geom_boxplot()
agedat_clean <- filter(agedat, age <= 100) # remove age > 100
ggplot(agedat_clean, aes(sex, age)) + geom_boxplot()
Go to Python notebook for Python version
Data wrangling (transformation, etc.)¶
Methods¶
We will cover basic statistical (and some machine learning) methods at a very basic level.
But,I expect that you are open to learning new statistical methods with minimal guidance.
Data analysis - Case study¶
Genetic Activity for Leukemia Patients¶
(Ref: CASI, pg. 8 - 10)
72 leukemia patients, 47 with ALL (acute lymphoblastic leukemia) and 25 with AML (acute myeloid leuk- emia, a worse prognosis) have each had genetic activity measured for a panel of 7,128 genes.
The data are shown below
leuk_dat <- read_csv("https://web.stanford.edu/~hastie/CASI_files/DATA/leukemia_big.csv")
leuk_dat %>% head()
The histograms and boxplots below show the distributions for gene 48 in the ALL and AML groups.
Exercise #1¶
Create the histogram and boxplots above using R or Python. Interpret each plot. Which plot do you prefer to compare the distributions? Why?
Is there a difference in gene 48 between patients with ALL (acute lymphoblastic leukemia) compared to AML(acute myeloid leukemia, a worse prognosis)?
Exercise #2¶
Use R or Python to calculate a p-value for a test comparing the two groups. Interpret the p-value.
This is one candidate gene out of 7,128 genes. Is $t=-3.30$ unusual?
Exercise #3¶
Create the histogram above using R or Python. Write a few sentences describing how the histogram above was generated. Is gene48 unusual compared to other genes?
Statistical Thinking and Hypothesis Testing¶
- The general ideas behind testing hypotheses permeate "statistical thinking".
- The core of statistical thinking includes the appreciation of uncertaintity and variability.
- Hospital A has 20 births per day and Hospital B has 50 births per day. During a period one year which hospital is more likely to have more than 60% boys born?
Exercise #4¶
During a period two years which hospital is more likely to have more than 60% boys born? Use R or Python to create similar histograms that show the distributions of boys in a large and small hospital.
Hypothesis Testing¶
- Let's look at the expression of gene 48 between the two groups, ALL and AML.
- Assume that there is no difference in gene expression between the two groups. This means that the same gene expression value for a patient would occur if that patient is in the ALL or AML groups.
set.seed(100)
gene_48 %>% select(value, group) %>% sample_n(5)
gene_48 %>% group_by(group) %>%
summarise(n = n(), mean = mean(value), sd = sd(value)) %>%
mutate(diff = mean - lag(mean))
- Under the assumption of no difference how likely is it that we would observe a difference of -3.30 (the observed difference)?
- Under the assumption of no difference the group labels
AMLandALLare interchangeable. The number of permutations of the lables is the number of ways that the observed data could have been generated under the assumption of no difference? - In this case there are ${{47+25} \choose 47} = 1.5 \times 10^{19}$.
- Instead of evaluating all $1.5 \times 10^{19}$ we can create a resampled permutation of the data set where we permute the group label. Then repeat this, say, 10000 times. (see pages 49-51, CASI)
options(repr.plot.width=6, repr.plot.height=3)
tibble(rs_dist) %>%
ggplot(aes(rs_dist)) + geom_histogram(colour = "black", fill = "grey", bins = 25) +
geom_vline(xintercept = -0.2269164, colour = "red") +
ggtitle("Permutation Null Distribution of Mean Difference") + xlab("Mean Difference") +
geom_text(aes(-0.2269164, 0, label = "-0.23", hjust = 1, vjust = 1.2), size = 3)
tibble(rs_dist) %>% summarise(pvalu = sum(rs_dist <= -0.2269164)/Numsim)
Exercise #5¶
Use R or Python to create the permutation distribution. Calculate the two-sided P-value? Briefly interpret the two-sided P-value.